Essay #6: A Better Benchmark for Hierarchical Risk Parity (HRP) Portfolios: Part 3
Simulations show that HRP's ignoring of correlations results in worse out-of-sample performance than the ERC benchmark.
This will be the final part of the “A Better Benchmark for Hierarchical Risk Parity” series.
To recap: both ERC and HRP, when naively implemented, might provide undesirable behavior. Both Part 1 and Part 2 demonstrate the most glaring failings:
HRP fails to incorporate correlations meaningfully, as the recursive bisection process can separate assets that were assigned to the same cluster.
ERC provides undesirable weights when 2 assets are near-duplicates of each other.
Thus, my purpose is neither to defend risk parity as an investment paradigm nor to defend one of {ERC, HRP} as a better method than the other.
My main gripes are with the apparent lack of editorial oversight in the Journal of Portfolio Management (JoPM) and with Marcos Lopez de Prado’s (MLdP) authoritative tone that borders on being in the Nassim Taleb tier of condescension1, despite the obvious problems with MLdP’s published work.
Parts 1 and 2 focused on in-sample features of ERC & HRP. Instead, in this essay we evaluate, via Monte Carlo simulations, the performance out-of-sample of HRP against ERC.
Simulations
This HRP_ERC_MC.py script takes MLdP’s HRP_MC.py code, and adds ERC code to the models to be included in the Monte Carlo simulations.
There are some really cool (and important) features of MLdP’s simulation infrastructure; here are highlights from the code’s comments:
#1) generate random uncorrelated data
#2) create correlation between the variables
#3) add common random shock
#4) add specific random shock
Obviously no one is claiming2 that this represents the entire data-generating process of financial asset returns; however, systematic shocks and idiosyncratic shocks are undoubtedly important features of real financial data.
Here is the JoPM summary of how the simulation is carried out:
In practice, firms will likely apply some “special sauce” in addition to the above, like increasing the influence of more recent data or applying statistical shrinkage3 techniques to address estimation error. What’s important here is that all of {HRP, IVP4, ERC} are given the same input covariance matrix. Massaging that input is a completely separate exercise5.
As each asset is constructed to have mean zero, the JoPM results of these simulations focus on the out-of-sample volatility6 of the resulting simulations:
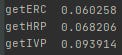
When we include ERC as a method, we get the following out-of-sample variances7:
While we don’t have the same seed8 as the JoPM simulation, the above results appear consistent with what was published in the JoPM: IVP out-of-sample variance was 0.093914 (0.0928 in JoPM), and HRP out-of-sample variance was 0.068206 (0.0671 in JoPM).
ERC provided the lowest out-of-sample variance: 0.060258, 7% lower than HRP’s out-of-sample variance.
Unlike IVP and HRP, ERC accounts for correlations in a meaningful way.
Final Thoughts
It’s worth repeating the chastising that MLdP & the JoPM push on their straw-man IVP benchmark, but repurposed for their own published HRP model:
Shocks involving several correlated investments penalize HRP’s ignorance of the correlation structure.
From these simulations, ERC provided better protection9 than HRP against both common and idiosyncratic shocks.
This variance reduction out-of-sample is critically important to risk parity investors, given their frequent use of leverage.
Appendix: Version Control / GitHub
Any code, data, and other artifacts produced for this essay will be saved here.
Standard disclaimer that I’ve met neither of these individuals in person, hence my hesitation for what may be perceived as slander. I just want to present good models and good research, but without being a jerk, and I recognize that communication is really difficult sometimes. That said, I think I’ve seen enough of the publicly available discourse that my priors have good reason to not be too diffuse.
If anyone does claim to know the entire DGP, please do let me know; I might be willing to pay 2 & 20.
Not the Costanza version.
Inverse Variance Portfolio, which I label a straw-man benchmark, not representative of actual risk parity portfolio implementations, in Part 1.
Minor gripe: it’s odd that MLdP/JoPM switch between volatility and variance in consecutive paragraphs. Yes you can derive one from the other, but just pick one and stick with it, as a courtesy to your readers.
Expressed as volatility: {ERC: 24.5%, HRP: 26.1%, IVP: 30.6%} . While each asset is initialized to 10% volatility, the shocks increase the realized volatility.
Again, kudos to MLdP for including the seed (12345) in his HRP.py (not HRP_MC.py) code.
As measured by out-of-sample volatility.